조합(Combination)
2021. 1. 31. 13:34ㆍ수학
조합이란 $n$개의 물건들 중 $k$개를 중복없이 순서를 고려하지 않고 뽑는 경우의 수를 의미한다.
$_{n}\mathrm{C}_{k}$
로 표기하며 계산법은 다음과 같다.
$\frac{n!}{(n-k)!(k!)}$
이 글에서는 $n$을 FN(Front Number) $k$를 RN(Rear Number)라고 정의하겠다.
각 조합의 계수는 $C(FN,RN)$이라고 표현하겠다.
$_{2n}\mathrm{C}_{k}$
1단계 : $=$$_{2n-1}\mathrm{C}_{k}$$+$$_{2n-1}\mathrm{C}_{k-1}$
2단계 : $=$$_{2n-2}\mathrm{C}_{k}$$+$$2\cdot_{2n-2}\mathrm{C}_{k-1}$$+$$_{2n-2}\mathrm{C}_{k-2}$
식을 보면 조합 1개가 2개로 나누어질 때마다 RN이 다른 각 조합 앞의 계수가 규칙적으로 변함을 알 수 있다.
식으로 표현하면 $n$ 단계에서
$C(n,k)+C(n,k-1)=C(n-1,k-1)$ $\cdot\cdot\cdot(1)$
이다. 이 식은 조합의 성질인
$_{n}\mathrm{C}_{k}$$=$$_{n-1}\mathrm{C}_{k}$$+$$_{n-1}\mathrm{C}_{k-1}$
과 비슷하다. 다른 점은 $(1)$은 파스칼의 삼각형의 순서를 상하, 좌우 대칭 시켜 놓은 것이다.


위 그림에서 $(n, k)=_{n}\mathrm{C}_{k}$ 를 나타낸 것이다.
파란색과 빨간색 순서에 유의하면 $(1)$의 식도 결국 조합을 나타내는 것임을 알 수 있다.
단계를 $n$번 반복하면
$_{2n}\mathrm{C}_{k}$
$=_{n}\mathrm{C}_{0}\cdot _{n}\mathrm{C}_{k}+_{n}\mathrm{C}_{1}\cdot _{n}\mathrm{C}_{k-1}+...+$$_{n}\mathrm{C}_{k-1}\cdot _{n}\mathrm{C}_{1}+_{n}\mathrm{C}_{k}\cdot _{n}\mathrm{C}_{0}$
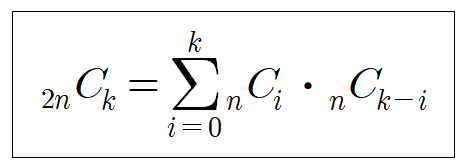
'수학' 카테고리의 다른 글
| 포물선 (0) | 2021.02.16 |
|---|---|
| 피보나치 수열 (1) | 2021.02.15 |
| 2차 잉여의 성질 & 오일러 판정법 (0) | 2021.01.29 |
| 윌슨의 정리 (0) | 2021.01.29 |
| 절댓값 합 함수(Ⅱ) (3) | 2021.01.26 |